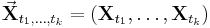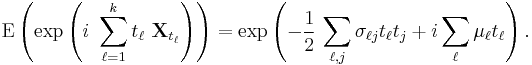Gaussian process

In probability theory and statistics, a Gaussian process is a stochastic process whose realisations consist of random values associated with every point in a range of times (or of space) such that each such random variable has a normal distribution. Moreover, every finite collection of those random variables has a multivariate normal distribution.

Gaussian processes are important in statistical modelling because of properties inherited from the normal. For example, if a random process is modelled as a Gaussian process, the distributions of various derived quantities can be obtained explicitly. Such quantities include: the average value of the process over a range of times; the error in estimating the average using sample values at a small set of times.

Contents

Definition

A Gaussian process is a stochastic process { Xt ; t ∈ T } for which any finite linear combination of samples will be normally distributed (or, more generally, any linear functional applied to the sample function Xt will give a normally distributed result).

Some authors[1] also assume the random variables Xt have mean zero.

History

The concept is named after Carl Friedrich Gauss simply because the normal distribution is sometimes called the Gaussian distribution, although Gauss was not the first to study that distribution: see history of the normal/Gaussian distribution.

Alternative definitions

Alternatively, a process is Gaussian if and only if for every finite set of indices t1, ..., tk in the index set T

\vec{\mathbf{X}}_{t_1, \ldots, t_k} = (\mathbf{X}_{t_1}, \ldots, \mathbf{X}_{t_k})

is a multivariate Gaussian random variable. Using characteristic functions of random variables, the Gaussian property can be formulated as follows:{ Xt ; t ∈ T } is Gaussian if and only if, for every finite set of indices t1, ..., tk, there are reals σl j with σi i > 0 and reals μj such that

\operatorname{E}\left(\exp\left(i \ \sum_{\ell=1}^k t_\ell \ \mathbf{X}_{t_\ell}\right)\right) = \exp \left(-\frac{1}{2} \, \sum_{\ell, j} \sigma_{\ell j} t_\ell t_j %2B i \sum_\ell \mu_\ell t_\ell\right).

The numbers σl j and μj can be shown to be the covariances and means of the variables in the process.[2]

Important Gaussian processes

The Wiener process is perhaps the most widely studied Gaussian process. It is not stationary, but it has stationary increments.

The Ornstein–Uhlenbeck process is a stationary Gaussian process.

The Brownian bridge is a Gaussian process whose increments are not independent.

The fractional Brownian motion is a Gaussian process whose covariance function is a generalisation of Wiener process.

Applications

A Gaussian process can be used as a prior probability distribution over functions in Bayesian inference.[3][4] (Given any set of N points in the desired domain of your functions, take a multivariate Gaussian whose covariance matrix parameter is the Gram matrix of your N points with some desired kernel, and sample from that Gaussian.) Inference of continuous values with a Gaussian process prior is known as Gaussian process regression, or Kriging.[5] Gaussian processes are also useful as a powerful non-linear interpolation tool. Gaussian processes can also be used for probabilistic classification[6].

See also

Notes

  1. ^ Simon, Barry (1979). Functional Integration and Quantum Physics. Academic Press. 
  2. ^ Dudley, R.M. (1989). Real Analysis and Probability. Wadsworth and Brooks/Cole. 
  3. ^ Rasmussen, C.E.; Williams, C.K.I (2006). Gaussian Processes for Machine Learning. MIT Press. ISBN 0-262-18253-X. http://www.gaussianprocess.org/gpml/. 
  4. ^ Liu, W.; Principe, J.C. and Haykin, S. (2010). Kernel Adaptive Filtering: A Comprehensive Introduction. John Wiley. ISBN 0470447532. http://www.cnel.ufl.edu/~weifeng/publication.htm. 
  5. ^ Stein, M.L. (1999). Interpolation of Spatial Data: Some Theory for Kriging. Springer. 
  6. ^ Rasmussen, C.E.; Williams, C.K.I (2006). Gaussian Processes for Machine Learning. MIT Press. ISBN 0-262-18253-X. http://www.gaussianprocess.org/gpml/. 

External links

Video tutorials